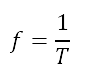The equation for period is:
Where:
T = period (s)
f = frequency (s
-1
, or Hz)

Period (T) and frequency (f)





Calculator
Period and Frequency
This page contains a period (T) calculator, as well as a calculator with the equation rearranged to make frequency (f) the
subject. The formulas are shown together with other useful information and examples to try.
The period (T) is the interval of time between successive occurrences of an event. This could be anything that has a
series of successive occurrences, such as the number of times a wave crest passes a certain point. This is especially
useful when considering the frequency of an occurrence, and the period is simply the reciprocal of the frequency, as
demonstrated by the calculators below. Unless otherwise stated the period T usually has a unit of seconds.
Enter all figures without commas. For example, enter 2,400 as 2400.
Period (T)
The equation for Period T is given on the right.
Example: When a cello is in standard tuning its lowest note is C2.
This has a frequency of 65.4 Hz. What is the period of this
frequency?
Entering 65.4 Hz into into the calculator and clicking Calculate shows
that the period is about 0.01529 seconds. In other words, wave
crests generated by the cello repeat about every 0.015 seconds
when this note is played.
The highest note on a cello is A5. This is 880 Hz. What is its period?
Frequency (f)
The equation for frequency is given above right.
Example: A radio wave has a time period of 0.000000322 seconds.
What is its frequency?
Using the calculator we can see that the frequency is 3,105,590 Hz,
or close to 3.1 MHz.
Radio waves range from about 20 kHz (the top of the range for
frequencies we can hear) to about 300 GHz (the lower end of
infrared frequencies) and are part of the electromagnetic spectrum.
The equation for frequency is:
Where:
f = frequency (s
-1
, or Hz)
T = period (s)

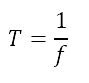
Advertisement




Calculator
Advertisement



Period and Frequency
Period (T) and frequency (f)

This page contains a period (T) calculator, as well as a calculator
with the equation rearranged to make frequency (f) the subject.
The formulas are shown together with other useful information
and examples to try.
The period (T) is the interval of time between successive
occurrences of an event. This could be anything that has a
series of successive occurrences, such as the number of times a
wave crest passes a certain point. This is especially useful when
considering the frequency of an occurrence, and the period is
simply the reciprocal of the frequency, as demonstrated by the
calculators below. Unless otherwise stated the period T usually
has a unit of seconds.
Enter all figures without commas. For example, enter 2,400 as
2400.
Period (T)
The equation for Period T is given below.
Example: When a cello is in standard tuning its lowest note is
C2. This has a frequency of 65.4 Hz. What is the period of this
frequency?
Entering 65.4 Hz into into the calculator and clicking Calculate
shows that the period is about 0.01529 seconds. In other words,
wave crests generated by the cello repeat about every 0.015
seconds when this note is played.
The highest note on a cello is A5. This is 880 Hz. What is its
period?
The equation for period is:
Where:
T = period (s)
f = frequency (s
-1
, or Hz)
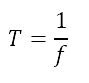
Frequency (f)
The equation for frequency is given below.
Example: A radio wave has a time period of 0.000000322
seconds. What is its frequency?
Using the calculator we can see that the frequency is 3,105,590
Hz, or close to 3.1 MHz.
Radio waves range from about 20 kHz (the top of the range for
frequencies we can hear) to about 300 GHz (the lower end of
infrared frequencies) and are part of the electromagnetic
spectrum.
The equation for frequency is:
Where:
f = frequency (s
-1
, or Hz)
T = period (s)